آخر تحديث: 30/03/2024
من هو مكتشف الباي وتاريخ اكتشاف π عبر الحضارات؟
من هو مكتشف الباي؟ يفتح هذا السؤال البسيط أبوابًا واسعة لاستكشاف عالم الرياضيات وتاريخها، فالباي ليس مجرد ثابت رياضي، بل هو لغز يحير عقول الفلاسفة والعلماء على مر العصور. تتعدد القصص والنظريات حول من اكتشف هذا العدد وكيف تم تحديده، مما يضفي مزيدًا من السحر والغموض على هذا العدد الذي يحمل العديد من الأسرار والخصائص المثيرة. مع موقع مفاهيم، هيا نتعرف على من هو مكتشف الباي!


من هو مكتشف الباي
من هو مكتشف الباي؟
- مكتشف الباي هو الرياضي اليوناني أرخميدس.
- كان أرخميدس، الذي عاش في القرن الثالث قبل الميلاد في اليونان، واحدًا من أعظم علماء الرياضيات في التاريخ القديم.
- قدم أرخميدس العديد من الأعمال الرياضية المهمة، بما في ذلك كتاب "قياسات الدائرة" (On the Measurement of the Circle)، الذي تناول فيه الدائرة وأبحاثها المتعلقة. في هذا الكتاب، قدم أرخميدس أحد أوائل الأدلة الهندسية لقيمة الباي.
- استخدم أرخميدس تقنيات الهندسة اليونانية القديمة، مثل تقسيم الدائرة إلى مثلثات ومضاعفة الزوايا، لتقدير قيمة الباي. على سبيل المثال، قام بتقديم تقدير لقيمة الباي بتقسيم محيط الدائرة إلى عدد من الأجزاء متساوية وقياس زوايا هذه الأجزاء.
- على الرغم من أن أرخميدس لم يقدم قيمة دقيقة للباي، فإن عمله وأسلوبه في اقتراب من القيمة الصحيحة قدم أساسًا مهمًا لاحقًا لعلماء الرياضيات لتطوير تقديرات دقيقة لقيمة الباي. وبهذا الشكل، أثرت أعمال أرخميدس في فهمنا الحالي للباي وأهميته في الرياضيات.
تعريف الباي
- الباي (π) هو ثابت رياضي يُمثل نسبة محيط الدائرة إلى قطرها، ويُعرف عادةً بالقيمة التقريبية 3.14159.
- تتمثل قيمة الباي في النسبة بين محيط الدائرة (مسافة حول الدائرة) وقطرها (المسافة عبر الدائرة من حافتها).
- على الرغم من أن القيمة التقريبية 3.14159 شائعة الاستخدام، إلا أن الباي له قيمة لا تنتهي وتتمثل في سلسلة من الأرقام اللا نهائية بعد الفاصلة العشرية.
تاريخ اكتشاف الباي
- يعود تاريخ اكتشاف الباي إلى العديد من الحضارات القديمة، ولكن أول ذكر لهذا العدد كمنسوب للدائرة كان من قبل الحضارة المصرية القديمة والتي قدرت قيمته بنسبة 3.16 تقريباً.
- بعدها، استخدم البابليون والهنود والصينيون تقديرات مختلفة للباي في حساباتهم الرياضية والهندسية.
- مع تقدم الرياضيات وتطورها في العصور القديمة، بدأت الحضارة اليونانية في التفكير بشكل عميق في الباي ودوره في الهندسة. من بين الفلاسفة اليونانيين، اشتهر أرخميدس بأعماله الرياضية التي تضمنت تقديرًا لقيمة الباي بطرق هندسية.
- تطورت دراسة الباي في العصور اللاحقة، وخلال القرون الوسطى، بدأت تظهر تقديرات أكثر دقة، مثل تلك التي أعطاها الرياضي الهندوسي أريابهاتا بقيمة تقريبية تساوي 3.1416.
- في العصور الحديثة، استمرت الجهود في حساب الباي بدقة أكبر، مما أدى إلى تطور العديد من الطرق الرياضية والحسابية لتقدير قيمته بشكل أكبر دقة، بما في ذلك استخدام الحاسبات الإلكترونية لحساب الأعداد بالباي إلى ملايين الأرقام العشرية.
تطبيقات الباي في العلوم المعاصرة
يلعب الباي (π) دورًا حيويًا في العلوم المعاصرة، حيث يستخدم في مجموعة متنوعة من التطبيقات، بما في ذلك:
- الهندسة: يستخدم الباي في حساب محيط الدوائر ومساحتها، بالإضافة إلى حساب حجوم الأشكال الثلاثية الأبعاد مثل الأسطوانات والكرات.
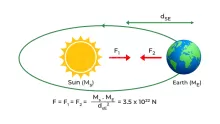
- الفيزياء: يظهر الباي في العديد من المعادلات الفيزيائية، مثل قانون الجاذبية لنيوتن وقانون الحركة الدائرية.
- الهندسة المرجحة: يستخدم الباي في تحليل البيانات والنماذج الإحصائية لتقدير الاحتمالات والانحرافات المعيارية.
- الهندسة الفلكية: يستخدم الباي في حسابات المسافات والأبعاد في الكون، مثل حجم الكواكب والنجوم والمجرات.
- الهندسة الكمية: يستخدم الباي في الحسابات الكمية والنمذجة الرياضية للتنبؤ بتفاعلات الجسيمات والتراكيب الذرية.
- تكنولوجيا المعلومات: يستخدم الباي في العديد من التطبيقات التقنية، مثل الشبكات العصبية الاصطناعية والتشفير الرقمي.
باختصار، يظهر الباي أهميته في مجموعة واسعة من التطبيقات العلمية والتكنولوجية، مما يجعله ذا أهمية بالغة في فهم العالم الطبيعي وتطوير التكنولوجيا الحديثة.
أسرار العدد باي
الباي (π) ليس فقط ثابت رياضي، بل يحمل أيضًا العديد من الأسرار والخصائص المثيرة، منها:
- لا يمكن تمثيله بكسر محدد: رغم أن قيمة الباي يمكن تقريبها باستخدام كسور مثل 22/7، إلا أنه لا يمكن تمثيله بكسر محدد.
- لا يمكن حسابه بدقة مطلقة: لا يمكن حساب الباي بدقة مطلقة باستخدام أي طريقة؛ لأنه عدد غير قابل للتمثيل بكسر محدد وله قيمة لا تنتهي بعد الفاصلة العشرية.
- يشترك في العديد من المجالات الرياضية والعلمية: يظهر الباي في العديد من المجالات مثل الهندسة والفيزياء والإحصاء وغيرها، ويُستخدم في حساب مساحات الأشكال الهندسية وحجوم الأجسام الثلاثية الأبعاد وغيرها.
- له علاقة بالدورات الطبيعية: يظهر الباي بشكل متكرر في الظواهر الطبيعية مثل دورات الأمواج وتوزيع النجوم في السماء، مما يجعله عنصرًا مهمًا في فهم العالم الطبيعي.
- يمتلك قيمة تقريبية معروفة: يعتبر 3.14159 تقريبا لقيمة الباي، وهي القيمة المستخدمة في معظم الحسابات العملية.
في ختام مقال من هو مكتشف الباي؟، ندرك أن الباي (π) ليس مجرد عدد رياضي بل رمز للإبداع والتحدي في عالم الرياضيات. رغم التحديات التي تواجه عملية حسابه، فإن أهميته تتجسد في تطبيقاته الواسعة في مجموعة متنوعة من العلوم والتكنولوجيا المعاصرة.
للإستفادة من هذا المقال انسخ الرابط
https://mafahem.com/sl_20975
تم النسخ
لم يتم النسخ