بحث عن الدوال وأنواعها

الدوال هي من أهم الأقسام التي توجد في علم الجبر، ويجب العلم أن ذلك العلم لا يعتمد على الأرقام وحسابها وعملياتها المختلفة فقط، ولكنه يحتوي أيضًا على العديد من المتغيرات والرموز والعلاقات التي ترتبط مع بعضها البعض، بالإضافة إلى أن الدوال تعمل على الربط بين مدخل ب مخرج محدد، سوف نقدم لكم من خلال موقعنا مفاهيم بحث عن الدوال.

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• ما مفهوم الدوال؟
• مقدمة بحث عن الدوال
• بحث عن الدوال وأنواعها
  • الدالة الثابتة
  • الدالة الجبرية
  • الدالة متعددة الحدود
  • الدالة التربيعية
  • الدالة التكعيبية
  • الدالة المحايدة
• ما هي شروط الدالة؟
• بحث عن الدوال المثلثية
• ماهي استخدامات الدوال المثلثية؟
• من هو مخترع الدوال المثلثية؟
• ما هي قيمة المثلث؟
• بحث عن الدوال والمتباينات
• أنواع المتباينات
• أهم الأسئلة الشائعة
  • متى يتم تغيير إشارة المتباينة؟
  • متى يتم قلب المتباينة؟
  • متى يكون الخط متقطع في تمثيل المتباينات الخطية؟
  • ما هو معنى المتباينة المثلثية؟
  • ما القيم التي تحققها المتباينات؟

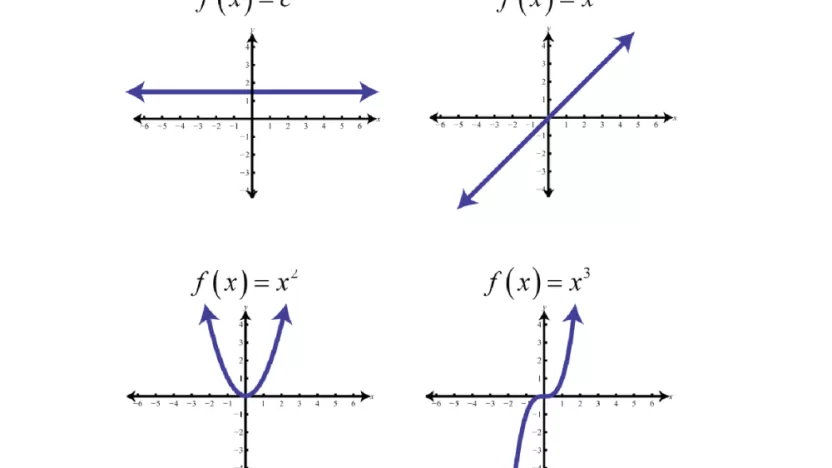
ما مفهوم الدوال؟

يجب العلم أن إجراء بحث عن الدوال والمتباينات معرفة أنها من أهم القواعد في علم الرياضيات والدوال، كما عرفها عالم الرياضيات الألماني بيتر ديريتشليت عام 1837 لأول مرة أنها علاقة ما بين كل من المدخلات والمخرجات، ومن الممكن أن يرتبط ذلك المدخل بمخرج واحد فقط أو يرتبط مخرج واحد بأكثر من مدخل، بمعنى عندما يكون المتغير y مرتبط بالمتغير x، يجب وضع قيمة عددية لكل من المتغيرين وفي تلك الحالة يكون y هو الدالة الخاصة بالمتغير x والقانون الخاص بها يكون y=f(x)v.

مقدمة بحث عن الدوال

تستخدم الدوال في وصف العلاقات بين متغيرين، بالإضافة إلى أنها تعمل على تحليل سلوك الظواهر في المجالات المختلفة الأخرى، ويجب أن تكون المجموعات التي يتم استخدام الدوال فيها أن تكون غير ممتلئة، مثال على ذلك:

أجد حل للدالة g(t)= 6t^2+5 وذلك عندما تكون

• t=0
• t=2

الإجابة عندما تكون t تساوي 0: g0= 6(0) ^2+5=5

الإجابة عندما تكون t تساوي 2: g2=6(2) ^2+5=29

بحث عن الدوال وأنواعها

يوجد العديد من أنواع الدوال الرياضية المختلفة والتي من أبرزها:

الدالة الثابتة

• وهي التي يكون فيها التابع الرياضي ثابت، ولا تتغير القيمة الخاصة به، والصيغة الخاصة بها هي: f(x)=a.

الدالة الجبرية

• وهي الدوال التي تكون عبارة عن متغيرات وعمليات حسابية، والتي تشمل الجمع والطرح والقسمة والأسس والجذور، وصيغتها: f(x)=x²+3x+6.

الدالة متعددة الحدود

• وفي ذلك النوع تحتوي الدالة على واحد أو أكثر من المتغيرات والمعاملات، والتي تتم أيضًا من خلال عمليات الطرح والقسمة والجمع والضرب، ويجب أن يكون الأس صحيح وليس سالب وصيغتها P(x)=anxn+an-1xn-1+...+a1x+a0.

الدالة التربيعية

• وفيها تحتوي الدالة على المتغيرات الثلاثة x,y,z، يكون لها حدود ثابتة والصيغة العامة لها هي f(x)=ax²+bx+c، أما في حالة أن تكون الدالة التربيعية أحادية المتغير والتي تكون بإضافة a أو b أو c أو d أو e أو f للحدود من الدرجة الثانية ولكن بشرط ألا يكون أي منهم يساوي 0.

الدالة التكعيبية

• وهي واحدة من الدوال كثيرة الحدود والصيغة العامة لها f(x)=ax³+bx²+cx+d.

الدالة المحايدة

• وتم تسميتها بذلك الاسم لأن تكون فيها f(x)=x، بمعنى أن تكون قيمة المتغير والصورة الخاصة به متساويين دائمًا، وعندما يتم التعويض برقم 1 يكون الناتج أيضًا 1 وعند التعويض برقم 2 يكون الناتج 2 وهكذا.

ما هي شروط الدالة؟

تكون دالة عند توفير شرطين أساسيين وهما:

1. أن يرتبط كل عنصر من المدخلات بقيمة مخرجه.
2. لا يجب أن يرتبط عنصر المدخلات بأكثر من عنصر في المخرجات.

بحث عن الدوال المثلثية

يتم استخدام الدوال المثلثية في حساب الزوايا وتطبيقاتها في علم المثلثات، وهي إحدى فروع الرياضيات وهم عبارة عن 6 زوايا، والتي تم التعرف عليهم بواسطة المثلث قائم الزوايا وهم:

1. جيب الزاوية sin وهي عبارة عن ناتج قسمة القيمة الخاصة بالضلع المقابل للزاوية على قيمة وتر المثلث القائم.
2. جيب التمام لزاوية cos والذي يكون ناتج قسمة الضلع المجاور للزاوية على قيمة وتر المثلث القائم.
3. ظل الزاوية tan والذي يكون ناتج قسمة قيمة الضلع المقابل للزاوية على قيمة الضلع المجاور للزاوية.
4. ظل تمام الزاوية cot وهو يكون عبارة عن ناتج قسمة قيمة الضلع المجاور للزاوية على قيمة الضلع المقابل للزاوية.
5. قاطع الزاوية sec والذي يكون ناتج قسمة وتر المثلث القائم على قيمة الضلع المجاور للزاوية.
6. قاطع تمام الزاوية csc وهو عبارة عن ناتج قسمة قيمة وتر المثلث القائم على قيمة الضلع المقابل للزاوية.

ماهي استخدامات الدوال المثلثية؟

• يتم استخدامها في حل المعادلات المثلثية.
• عندما تكون الزوايا حادة يتم استخدامها في إيجاد قيمة الزاوية المجهولة.

من هو مخترع الدوال المثلثية؟

• أبر خش وهو الذي قام بإنشاء أول جدول مثلثي وأطلق عليه أبي الحساب.

ما هي قيمة المثلث؟

• مجموع الزوايا الداخلية للمثلث هي 180 درجة.

بحث عن الدوال والمتباينات

المتباينات والتي يطلق عليها أيضًا المتراجحات تستخدم في المقارنة بين قيمتين مختلفتين، وذلك بحيث تكون قيمة أكبر من أو أقل أو لا تساوي القيمة الأخرى، بمعنى:

• أ≥ ب المقصود بها أن أ أكبر من أو تساوي ب.
• أ ≠ب تعني أن أ لا تساوي ب.
• أ ≤ب تعني أن أ أصغر من أو تساوي ب.
• أ<ب المقصود بها أن أ أصغر من ب.
• أ>ب تعني أن أ أكبر من ب.

أنواع المتباينات

يوجد 3 أنواع أساسية من المتباينات وهم:

1. المتباينات الخطية: ومعناها في علم الرياضيات عدم المساواة وهي تعمل على مقارنة غير متساوية ما بين متغيرين رياضيين أو رقمين، وفي بعض الأحيان يكون عدم المساواة إما عدم مساواة عددية أو عدم مساواة جبرية أو مزيج ما بين النوعين.
2. المتباينات الغير خطية: وهي تشمل المعادلات الغير خطية مثل: المقاطع المخروطية، كما أنها تعرف أيضًا بأنها المعادلة التي تحتوي على قيمة التي يتم رفعها على الأقل إلى قوة 2، بالإضافة إلى أن ينتج عن تلك المعادلة خطوط منحنية في الرسومات البيانية، من أكثر طرق الحل انتشارًا لذلك النوع هو استخدام التعويض وذلك بسبب احتوائها على مصطلحات غير متشابهة.
3. المتباينات الكسرية: هي المتباينات التي تحتوي على كسور ويجب عند حل ذلك النوع ضرب جميع القيم بالموجب.

أهم الأسئلة الشائعة

متى يتم تغيير إشارة المتباينة؟

• في حالة الضرب في ناقص واحد يتم تغيير إشارة المتباينة من أكبر من أو يساوي إلى أصغر من أو يساوي.

متى يتم قلب المتباينة؟

• في حين الحصول على عدد صحيح يجب تغيير إشارة المتباينة.

متى يكون الخط متقطع في تمثيل المتباينات الخطية؟

• عندما تكون لا تشمل علامة التساوي.

ما هو معنى المتباينة المثلثية؟

• هي التي تثبت أن أحد أضلاع المثلث أصغر من مجموع الضلعين الآخرين.

ما القيم التي تحققها المتباينات؟

• عندما تكون علامة المتباينة أكبر من أو يساوي يتم رسم خط متصل، وعندما تكون أكبر من فقط أو أصغر من فقط يتم رسم خط متقطع.