العوامل المؤثرة في قانون الكثافة وأهم الأمثلة عليه
جدول المحتويات
تعريف قانون الكثافة
- قانون الكثافة هو مبدأ أساسي في الفيزياء والكيمياء يصف العلاقة بين الكتلة والحجم لمادة معينة. يُعرّف الكثافة بأنها كمية الكتلة في وحدة الحجم للمادة.
- الكثافة هي مقياس لكمية المادة الموجودة في وحدة حجم معين. تُعبر عن كثافة مادة معينة بأنها كتلتها لكل وحدة حجم.
- ويمكن أن تساعد الكثافة في تحديد المواد ومعرفة ما إذا كانت هناك شوائب. وفي الكيمياء، تُستخدم الكثافة في حسابات التحليل وتحديد تركيز المحاليل.
- في الفيزياء، تلعب الكثافة دورًا في فهم سلوك المواد تحت تأثيرات مختلفة مثل الجاذبي
قانون الكثافة
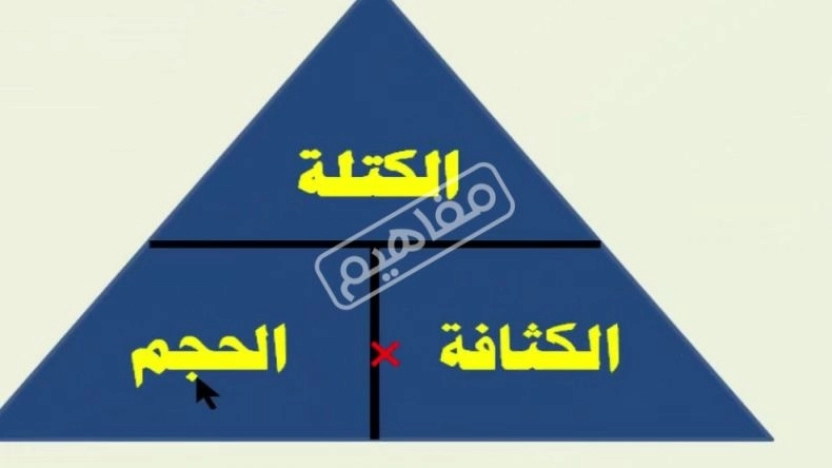
يمكن التعبير عنه رياضيا من خلال:
ρ = m/V.
- ρ : رمز يعبر عن الكثافة.
- m: الكتلة وتقاس بوحدة الغرام (غم).
- V: الحجم ويقاس بسنتيمتر مكعب(سم 3).
قانون الكثافة للسوائل
قانون الكثافة للسوائل يُعبر عن العلاقة بين الكتلة والحجم للسائل. الصيغة الأساسية للكثافة هي:
p= v/m
- ρ هو الكثافة.
- هو الكتلة.
- هو الحجم.
الشرح:
- الكثافة (Density) هي كمية تصف مدى تراص جزيئات المادة في وحدة الحجم.
- الكتلة (Mass) هي مقدار المادة الموجودة في الجسم.
- الحجم (Volume) هو المساحة التي يشغلها السائل.
وحدة الكثافة:
- في النظام الدولي للوحدات، وحدة الكثافة هي كيلوغرام لكل متر مكعب (kg/m³).
- في بعض الحالات، قد تُستخدم جرام لكل سنتيمتر مكعب (g/cm³) أيضًا.
مثال توضيحي:
إذا كان لديك سائل بكتلة 200 جرام وحجم 250 ملليلتر، فإن كثافة السائل تكون:
- (p) كثافة السوائل= 200 جم / 250 مل = 0.8 جم/ مل.
قانون الكتلة الحجمية
- قانون الكتلة الحجمية، المعروف أيضًا بقانون الكثافة، هو نفس ما شرحناه سابقًا. يُعبر عن العلاقة بين الكتلة والحجم لمادة معينة.
- في النظام الدولي للوحدات، وحدة الكتلة الحجمية هي كيلوغرام لكل متر مكعب (kg/m³).
- في بعض الأحيان تُستخدم وحدات أخرى مثل جرام لكل سنتيمتر مكعب (g/cm³) أو جرام لكل ميلليلتر (g/mL).
قانون الكتلة
قانون الكتلة هو مفهوم أساسي في الفيزياء والكيمياء يعبر عن كمية المادة الموجودة في جسم أو مادة معينة. النص العام لقانون الكتلة هو:
"الكتلة هي مقياس لكمية المادة في جسم ما، وهي خاصية ثابتة لا تتغير بتغير الموقع أو الظروف البيئية."
- الكتلة لا تحتاج إلى صيغة خاصة لأنها تعتبر كمية أساسية، ولكن يمكن التعبير عنها في معادلات مختلفة.
- في النظام الدولي للوحدات، وحدة الكتلة هي كيلوغرام (kg).
- في بعض السياقات، قد تُستخدم وحدات أخرى مثل جرام (g) أو مليمتر (mg).
قانون الوزن والكثافة
قانون الوزن والكثافة يرتبط ببعضه البعض من خلال العلاقة بين الكتلة والحجم. يمكن تلخيص العلاقة بين الوزن والكثافة بالصيغة التالية:
الوزن (Weight) هو القوة الناتجة عن تأثير الجاذبية على الكتلة. يُعطى بالصيغة: W=m.
- W هو الوزن.
- هو الكتلة.
- هو تسارع الجاذبية (عادةً 9.81 m/s² على سطح الأرض).
الكثافة (Density) تُعرّف بالعلاقة: ρ= V \
- هو الكثافة.
- m هو الكتلة.
- هو الحجم.
والجمع بين القوانين ينتج عنه الآتي:
يمكن استخدام الكثافة لربط الوزن بالحجم من خلال صيغة الجمع بين القوانين:
- احسب الكتلة باستخدام الكثافة والحجم:
- ثم احسب الوزن: W=m⋅g=(ρ⋅V)⋅g
لذا، صيغة الوزن بناءً على الكثافة والحجم هي:
W=ρ⋅V⋅g
قانون الكثافة في الكيمياء
في الكيمياء، يُعرّف قانون الكثافة بشكل مشابه كما في الفيزياء، ولكن يتم التركيز بشكل أكبر على المواد الكيميائية والسوائل. الصيغة العامة للكثافة هي:
ρ=m/V
- ρ هي الكثافة (Density).
- هي الكتلة (Mass).
- هو الحجم (Volume).
أما في حساب الكثافة من الكتلة الحجمية:
- في الكيمياء، إذا كنت تعرف الكتلة الحجمية (الكتلة لكل مول من المادة)، يمكنك حساب الكثافة باستخدام الصيغة: ρ=الكتلة المولية/الحجم المولّي
- إذا كان لديك سائل بكتلة 250 جرام وحجم 500 ملليلتر، فإن الكثافة تُحسب كما يلي:
الكثافة =250 جم/ 500 مل=0.5 جم/ مل
العوامل المؤثرة في الكثافة
من المعروف أن الكثافة تعتمد على خاصيتين فقط وهما الكتلة والحجم حيث أن الكثافة تتأثر بتأثرهما، ويجب العلم بأن الكتلة ثابتة فهي لا تقوم بأحداث تغيير على المادة. العامل الذي يتغير هو الحجم حيث أن الحجم سوف يتأثر بالعوامل الخارجية التي بعد ذلك تؤثر على المادة، فمن خلال قانون الكثافة يتم معرفة العلاقة العكسية التي تقوم بربط الحجم بالكثافة حيث عندما يزيد الحجم فسوف تقل الكثافة.
فالعوامل التي تؤثر في الكثافة هي:
أولاً: الحرارة
- فعندما يحدث أن يتعرض أي جسم للحرارة فإن جزيئاته سوف تمتلك طاقة عالية، وسوف تبتعد جزيئاته عن بعضها البعض فينتج عن ذلك زيادة في حجم الجسم مما يؤدي إلى حدوث نقصان في كثافة الجسم.
- فبالتالي فان العلاقة التي تكون بين الحرارة والحجم تكون علاقة طردية ولكن العلاقة التي تكون بين الحرارة والكثافة تكون علاقة عكسية.
ثانياً: الضغط
- عندما يحدث أن يتعرض الجسم إلى ضغط زيادة عليه، فيوف تتراص جزيئاته وسوف يحدث لها اقتراب من بعضها البعض فهذا يؤدي إلى نقصان في حجم الجسم، فبالتالي سوف تزداد كثافة الجسم، فبالتالي العلاقة بين الضغط والحجم تكون علاقة عكسية وأيضا العلاقة بين الضغط والكثافة تكون علاقة عكسية أيضا.
- فبالتالي فان كثافة المادة يتم تحديدها في جداول ولكن مع القيام بتحديد كلا من درجة الحرارة والضغط الذي يؤثر عليها ,فيجب العلم أن المواد الصلبة هي المواد التي تكون الأعلى كثافة.
- ثم بعد ذلك تليها المواد السائلة وفي النهاية تأتي المواد الغازية وهذا بسبب وجود اختلافات في المسافات التي تكون بين جزيئات كل حالة.
مثال:
لكي يتم توضيح كيف يتم الحصول علي كثافة جسم ما، فيمكن أن نفترض أن لدينا قطعة من الملح تكون بأبعاد 10 سم، 10 سم، 2 سم وهذه القطعة تزن 433غ، ولكي يتم حساب كثافة هذه القطعة فيجب أن يتم استخدام قانون الكثافة الآتي:
الكثافة = الحجم ÷ الكتلة.
ولكي يتم حساب حجم قطعة الملح يجب أن يتم استخدام قانون الحجم الذي يقوم بالاعتماد على شكل الأجسام، وهو :
الحجم= الطول*العرض*الارتفاع الحجم= 10*10*2 = 200 سم3.
وعندما يتم حساب حجم الجسم وأيضا معرفة كتلة الجسم المذكورة فيمكن أن يتم حساب كثافة الجسم كما يلي:
الكثافة = الحجم ÷ الكتلة الكثافة ,فهي = 433غ ÷ 200سم3 ,فان الكثافة = 2.165 غ/ سم3 ,فاذا كثافة قطعة الملح تساوي 2.615 غ/ سم3.
تطبيقات عملية على الكثافة
توجد العديد من التطبيقات لكي يتم تحديد قيم كثافة الأجسام المختلفة، فمن أهم هذه التطبيقات العملية في عملية تحديد قيم كثافة الأجسام المختلفة، هي:
أولاً: السفن والغواصات
- من أحد أهم تطبيقات الكثافة العملية هو القيام بتحديد سلوك الأجسام التي توجد في الماء، حيث أن بعض الأجسام سوف تطفو فوق الماء لأنها تكون أقل كثافة من كثافة الماء ولكن البعض الآخر سوف يغرق لأن كثافته سوف تكون أقل من كثافة الماء.
- تطفو السفن على سطح الماء نظرا إلى أنها تمتلك ثقل توازني يكون في قاع السفينة يتم تسميته بخزانات الموازنة (ballast tanks) والتي تكون عبارة عن صهاريج تكون مليئة بالهواء فيكون لها حجم كبير جدا وكتلة صغيرة جدا.
- فذلك يعني أن الكثافة تكون قليلة وهذا يكون أيضا نتيجة لعملها، وأيضاً بالإضافة إلى قوة الطفو التي تقوم بممارستها المياه على السفينة حيث أن السفينة تكون قادرة على الطفو على وجه الماء، حيث أن الغواصات أيضا يمكنها أن تغوص في أعماق المياه من خلال قيامها بعملية التخلص من هذه الخزانات.
ثانياً: الأنابيب
- عندما يتم تدفق الموائع من خلال الأنابيب ,فذلك من التطبيقات الهامة للكثافة والتي يتم التعبير عنها من خلال قانون برنولي، فهذا القانون يقول أن كثافة المائع سوف تقوم بالتأثير على سرعة الموائع وضغطها وأيضا ارتفاعها.
- فنتيجة لذلك فان الموائع التي يتم تدفيقها سوف تكون ذات كثافة مرتفعة وسوف يقل ضغطها وسرعتها وارتفاعها على نحو متتالي.
- فالمهندسون بشكل عام وكبير يقوموا بالاعتماد على معادلة برنولي لكي يتم تصميم السدود الكبيرة وأيضا يتم تصميم أنظمة الأنابيب المعقدة.
ثالثاً: توزيع وزن الطائرة
- من المعروف أن قدرة الطائرة تكون معتمدة على الطيران من خلال اعتمادها علي الضغط والسرعة، ويجب العلم أن الكثافة أيضا تقوم بلعب دور كبير وإضافي في هذه العملية أيضا.
- لأن القيام بتوزيع الأوزان التي توجد على متن الطائرة سوف يتم تغيره باستمرار نتيجة لاستهلاك الوقود في المحركات في أثناء عملية الطيران، فيجب العلم بأن كثافة الطائرة تكون غير متساوية في كافة أرجاء الطائرة.
- فعندما يتم فقدان الوزن فسوف يحدث تغير في مركز الكتلة بشكل مستمر فيجب علي الطيارين أن يقوموا بعملية مراقبة هذا التغير الذي يحدث بشكل مستمر وأيضا يجب أن يقوموا بالتعديلات الضرورية والكثيرة لكي يتم الحفاظ على طيران الطائرة.
بعض التطبيقات العملية الأخرى على الكثافة
- من أهم التطبيقات الأخرى للكثافة أنها تقوم بمعرفة كمية الشحن التي توجد في بطارية السيارة، حيث أن الطاقة التي يتم توليدها تعتمد على التفاعلات الكيميائية، وأيضا تعتمد علي انخفاض كثافة المحلول إشارة إلى أن يتم تفريغ الشحنات منه.
- يتم استخدام الكثافة في عملية الكشف عن بعض الأمراض، مثل: فحص الدم للكشف عن الأمراض؛ حيث أن للدم كثافة معينة وزيادة هذه الكثافة تدل على وجود تجمع كريات الدم الحمراء فهذه تكون إشارة عن وجود إصابة بمرض ما، مثل: مرض النقرس أو التهاب المفاصل أو يمكن أن يكون بسبب الجفاف أو قلة السوائل في الجسم أو فحص البول كما أن زيادة كثافته تدل على وجود ارتفاع في مستوى الأملاح فيه.
- تدخل الكثافة أيضا في عملية تصنيع الكثير من الآلات فيكون من أهمها الطائرات، فقد تم اختيار الألمنيوم ليكون هو هيكل الطائرة نظرا لانخفاض كثافته، فالكتلة الكلية في الطائرة يكون موضوع مهم للغاية,
للإستفادة من هذا المقال انسخ الرابط
https://mafahem.com/sl_11370