الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل

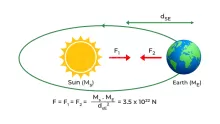
يُعد الزمن الدوري للكواكب أحد أهم المفاهيم في علم الفلك، حيث يحدد المدة التي يستغرقها الكوكب ليكمل دورة كاملة حول الشمس. وقد تناول قانون كبلر الثالث هذا الموضوع موضحًا العلاقة الرياضية بين الزمن الدوري للكوكب والمسافة التي تفصله عن الشمس. هذه العلاقة تكشف أن حركة الأجرام السماوية ليست عشوائية، بل تخضع لقوانين دقيقة يمكن من خلالها التنبؤ بمساراتها. وفي هذا المقال في موقع مفاهيم نتعرف على حل سؤال الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل، تابعونا.

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل
• الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل: كتلة الكوكب مكعب نصف قطر المدار كتلة الشمس ثابت الجذب الكوني؟
• يدور نبتون حول الشمس بنصف قطر m1012×495.4 فإذا كانت كتلة الشمس gk1030×99.1 يكون الزمن الدوري لنبتون
• يدور نبتون حول الشمس بنصف قطر ٤٩٥.٤ × ١٠¹² م، فإذا كانت كتلة الشمس ١.٩٩ × ١٠³⁰ كجم، فكم يكون الزمن الدوري لنبتون؟ ١) ٠.١٩ × ١٠⁻⁶ ث ٢) ٥.١٩٤ × ١٠⁶ ث ٣) ٢٦.٩٧ × ١٠⁶ ث ٤) ٤.٢٩ × ١٠⁶ ث؟
• حسب قانون كبلر الثالث فإن الزمن الدوري T لكوكب حول الشمس يتناسب مع بعده عن الشمس r حسب التالي
• إذا زادت كتلة الشمس للضعف فإن جذبها للمريخ
• الزمن الدوري لقمر اصطناعي يدور حول الأرض يتناسب
• ما هو الزمن الدوري؟
• ما هو قانون حساب الزمن الدوري؟
• العوامل المؤثرة على الزمن الدوري لدوران كوكب حول الشمس:

الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل

الجواب الصحيح يكون هو: الجذر التربيعي لمكعب نصف قطر.

الزمن الدوري لكوكب يدور حول الشمس يتناسب طرديًا مع الجذر التربيعي لمكعب نصف القطر،وهذا ما يُعرف بـ القانون الثالث لكبلر (Kepler’s Third Law)، والذي ينص على:

• الزمن الذي يستغرقه الكوكب ليدور دورة كاملة حول الشمس (الزمن الدوري) يتناسب طرديًا مع الجذر التربيعي لمكعب المسافة المتوسطة بين الكوكب والشمس.
• بمعنى أبسط: كلما ابتعد الكوكب عن الشمس، زادت الفترة التي يحتاجها ليكمل دورة واحدة حولها، والعلاقة بينهما ليست خطية، بل مرتبطة بالجذر التربيعي لمكعب المسافة.

مثال للتوضيح:

• الأرض: تدور حول الشمس على مسافة متوسطة تقارب 150 مليون كيلومتر، وتحتاج إلى سنة واحدة تقريبًا لتكمل دورة كاملة.
• المشتري: أبعد بكثير عن الشمس (حوالي 778 مليون كيلومتر)، لذلك يحتاج إلى حوالي 12 سنة ليكمل دورة كاملة.

هذا المثال يبين أن: كلما زادت المسافة بين الكوكب والشمس، زاد الزمن الدوري الذي يستغرقه الكوكب ليكمل دورة واحدة. وهذا بالضبط ما يوضحه القانون الثالث لكبلر.

الزمن الدوري لكوكب يدور حول الشمس يتناسب طردياً مع الجذر التربيعي ل: كتلة الكوكب مكعب نصف قطر المدار كتلة الشمس ثابت الجذب الكوني؟

الإجابة هي: مكعب نصف قطر المدار

الزمن الدوري للكوكب حول الشمس يتناسب طرديًا مع الجذر التربيعي لمكعب نصف قطر المدار، أي أن الكوكب كلما كان أبعد عن الشمس (أكبر نصف قطر للمدار)، كان زمن دورانه أطول.

باقي الخيارات ولماذا هي غير صحيحة:

1. كتلة الكوكب ❌ كتلة الكوكب لا تؤثر بشكل ملحوظ على زمنه الدوري حول الشمس. المدار وزمن الدوران يحددهما بشكل رئيسي بُعد الكوكب عن الشمس.
2. مكعب نصف قطر المدار ✅ هذه هي الإجابة الصحيحة حسب القانون الثالث لكبلر: الزمن الدوري يتناسب طرديًا مع الجذر التربيعي لمكعب نصف قطر المدار.
3. كتلة الشمس ❌ كتلة الشمس ثابتة لجميع الكواكب، لذا لا تفسر اختلاف الأزمنة الدورية بينها.
4. ثابت الجذب الكوني ❌ هذا ثابت فيزيائي عام لا يتغير (قيمته ثابتة في كل مكان)، وبالتالي لا يفسر اختلاف الأزمنة الدورية للكواكب.

يدور نبتون حول الشمس بنصف قطر m1012×495.4 فإذا كانت كتلة الشمس gk1030×99.1 يكون الزمن الدوري لنبتون

الإجابة هي: 2.697× 10¹² ثانية

يدور نبتون حول الشمس بنصف قطر ٤٩٥.٤ × ١٠¹² م، فإذا كانت كتلة الشمس ١.٩٩ × ١٠³⁰ كجم، فكم يكون الزمن الدوري لنبتون؟ ١) ٠.١٩ × ١٠⁻⁶ ث ٢) ٥.١٩٤ × ١٠⁶ ث ٣) ٢٦.٩٧ × ١٠⁶ ث ٤) ٤.٢٩ × ١٠⁶ ث؟

ما هو الزمن الدوري؟

الزمن الدوري هو الفترة الزمنية التي يستغرقها الكوكب لإكمال دورة كاملة حول الشمس.

• مثال: الأرض زمنها الدوري = سنة واحدة (365 يومًا).
• المشتري زمنه الدوري ≈ 12 سنة أرضية.

ما هو قانون حساب الزمن الدوري؟

• حسب القانون الثالث لكبلر: الزمن الدوري للكوكب يتناسب طرديًا مع الجذر التربيعي لمكعب نصف قطر المدار.
• بصياغة مبسطة: إذا عرفت المسافة بين الكوكب والشمس، يمكنك حساب الزمن الدوري من خلال العلاقة: كلما زاد نصف قطر المدار، زاد الزمن الدوري.

العوامل المؤثرة على الزمن الدوري لدوران كوكب حول الشمس:

1. المسافة بين الكوكب والشمس (نصف قطر المدار): العامل الأساسي، فكلما ابتعد الكوكب عن الشمس زاد زمنه الدوري.
2. كتلة الشمس: بما أنها ثابتة لجميع الكواكب في نظامنا، فهي العامل المركزي الذي يحدد قوة الجاذبية.
3. ثابت الجذب الكوني: ثابت فيزيائي يصف قوة الجاذبية، قيمته ثابتة ولا تتغير.

ملاحظة: كتلة الكوكب نفسها لا تؤثر بشكل ملحوظ على زمنه الدوري، لأن كتلة الشمس أكبر بكثير وتسيطر على الجاذبية.