تعرف على خصائص متوازي الأضلاع وطريقة حساب محيطه ومساحته

هل تعلم ما هي خصائص متوازي الأضلاع؟ هذا الشكل الهندسي المدهش ينبض بالتناغم الهندسي، فما هي خصائصه الفريدة؟ إن متوازي الأضلاع يتميز بزواياه الذهبية التي تبث فينا شعورًا بالتوازن والانسجام. بينما يلتقي ضلع بضلع، ينبعث الأمل في النظام والتناغم. سرٌ مدهش يكمن في مجموع قياسات زواياه، حيث يكمل بعضه بعضًا ليكوِّن دورة كاملة. في مفاهيم، انغمس في عالم الهندسة الساحر واكتشف خصائص متوازي الأضلاع.

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• ما هو متوازي الأضلاع وأنواعه؟
• خصائص متوازي الأضلاع
  • بحيث تُـكمل خصائص متوازي الأضلاع :
• مجموع زوايا متوازي الأضلاع
• المحيط والمساحة في متوازي الأضلاع
  • 1. حساب محيط متوازي الأضلاع
  • 2. حساب مساحة متوازي الأضلاع
• شروط يجب توافرها في متوازي الأضلاع

ما هو متوازي الأضلاع وأنواعه؟

متوازي الأضلاع هو شكل هندسي رباعي الأضلاع، يتميز بخصائص محددة، أهمها:

1. الأضلاع المتقابلة متوازية: في متوازي الأضلاع، الأضلاع المتقابلة تكون متوازية بعضها مع بعض.
2. الأضلاع المتقابلة متساوية في الطول: كل زوج من الأضلاع المتقابلة في متوازي الأضلاع له نفس الطول.
3. الزوايا المتقابلة متساوية: الزوايا المتقابلة في متوازي الأضلاع تكون متساوية في القياس.
4. مجموع الزوايا الداخلية = 360 درجة: كما هو الحال مع جميع الأشكال الرباعية، فإن مجموع الزوايا الداخلية لمتوازي الأضلاع يساوي 360 درجة.
5. القطريان يتقاطعان في منتصف الشكل: القطريان في متوازي الأضلاع يتقاطعان في نقطة المنتصف، مما يعني أن كل قُطر يقسم الآخر إلى جزئين متساويين.

صيغة حساب المساحة:

لحساب مساحة متوازي الأضلاع، يتم استخدام الصيغة التالية:

• المساحة=القاعدة×الارتفاع
• القاعدة هي طول أحد الأضلاع.
• الارتفاع هو المسافة العمودية بين القاعدة والضلع المقابل.

مثال:

• إذا كانت قاعدة متوازي الأضلاع 5 وحدات وارتفاعه 3 وحدات، فالمساحة تكون:
• المساحة=5×3=15 وحدة مربعة

خصائص متوازي الأضلاع

متوازي الأضلاع هو شكل مسطح ثنائي الأبعاد يتميز ببعض الخصائص الفريدة، ومن هذه الخصائص ما يلي:

1. يتكون متوازي الأضلاع من 4 أضلاع

• حيث يتقابل كل ضلعين متقابلين ومتساويين في الطول ومتوازيين في الاتجاه.

2. الزوايا المتقابلة متساوية

• أحد الخصائص الأساسية لمتوازي الأضلاع هو أن كل زاويتين متقابلتين متساويتين، مما يعني أن قياس زوايا المتوازي الأضلاع متساوٍ. بالإضافة إلى ذلك، إذا كانت إحدى الزوايا قائمة (قياسها 90 درجة)، فإن جميع الزوايا الأربعة ستكون قوائم، مما يجعل المتوازي الأضلاع في هذه الحالة مستطيلاً أو مربعًا.
• هناك 3 أنواع رئيسية من متوازي الأضلاع هي المستطيل، المعين، والمربع. المستطيل هو متوازي الأضلاع الذي يتمتع بأربعة زوايا قوائم، بينما المعين هو متوازي الأضلاع الذي يتمتع بأربعة أضلاع متساوية الطول وزوايا قائمة. أما المربع، فيتمتع بجميع خصائص المستطيل والمعين، حيث تكون أطوال أضلاعه متساوية وزواياه قوائم ومتعامدة.

3. الأضلاع المتقابلة متوازية:

• في متوازي الأضلاع، الأضلاع المتقابلة تكون متوازية بعضها مع بعض.

4. الأضلاع المتقابلة متساوية في الطول:

• كل زوج من الأضلاع المتقابلة في متوازي الأضلاع له نفس الطول.

5. مجموع الزوايا الداخلية = 360 درجة:

• كما هو الحال مع جميع الأشكال الرباعية، فإن مجموع الزوايا الداخلية لمتوازي الأضلاع يساوي 360 درجة.

6. القطريان يتقاطعان في منتصف الشكل:

• بالإضافة إلى الخصائص الأساسية المذكورة، متوازي الأضلاع يحتوي أيضًا على قطرين. القطر هو الخط المستقيم الذي يمكن رسمه بين رأسين متقابلين في متوازي الأضلاع، ويتميز القطرين بأنهما متساويان في الطول وكل قطر يقسم متوازي الأضلاع إلى مثلثين متطابقين.

7. الزوايا المتجاورة مجموعها 180 درجة:

• الزوايا التي تشترك في نفس الرأس (الزوايا المتجاورة) تكون مجموعها دائمًا 180 درجة.

بحيث تُـكمل خصائص متوازي الأضلاع :

القطران لا يكونان عموديين على بعضهما البعض بشكل عام:

• في متوازي الأضلاع، القطران لا يتقاطعان بزاوية 90 درجة (إلا إذا كان الشكل مربعًا). في الغالب، القطران يتقاطعان بزاوية غير قائمة.

تساوي المسافة بين الأضلاع المتوازية في أي نقطة:

• بما أن الأضلاع المتقابلة متوازية، فإن المسافة بين الأضلاع المتوازية تبقى ثابتة في جميع النقاط.

التماثل الجانبي:

• إذا قمت بثني الشكل على أحد أضلاعه، ستتطابق الأضلاع المتقابلة. يُظهر متوازي الأضلاع تماثلًا جانبيًا، حيث الأبعاد والاتجاهات تكون متشابهة على الجانبين المتقابلين.

أقطار متوازي الأضلاع تنقسم إلى جزئين متساويين:

• كل قُطر في متوازي الأضلاع يقسم القُطر الآخر إلى جزئين متساويين، مما يميز متوازي الأضلاع عن غيره من الأشكال الرباعية.

الأضلاع الزاوية:

• الأضلاع المجاورة للزاويتين الحادتين (الأقل من 90 درجة) تكون أقصر من الأضلاع المجاورة للزاويتين المنفرجتين (أكبر من 90 درجة)، لكن هذه الأضلاع تظل متساوية في الطول على الجانبين المتقابلين.

مجموع زوايا متوازي الأضلاع

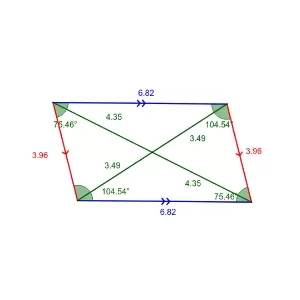
• متوازي الأضلاع هو شكل ثنائي الأبعاد يتكون من 4 أضلاع متوازية ذات أزواج من الأضلاع المتساوية في الطول والمتقابلة في الزوايا. واحدة من الخصائص المشتركة المهمة بين متوازي الأضلاع والأشكال الرباعية الأخرى هي مجموع زواياه.
• في متوازي الأضلاع، يكون لدينا اثنتان من الزوايا المتقابلة المتساوية. بشكل أكثر تحديدًا، الزوايا المتقابلة في متوازي الأضلاع تكون متساوية في القيمة ومجموعها يكون 360 درجة.
• مثلاً، إذا كانت إحدى الزوايا المتقابلة في متوازي الأضلاع تساوي 90 درجة، فإن الزاوية المقابلة لها ستكون أيضًا تساوي 90 درجة. وبالتالي، يكون مجموع زوايا متوازي الأضلاع هو 90 + 90 + 90 + 90 = 360 درجة.
• تلك الخاصية تنطبق على جميع أنواع متوازي الأضلاع، بغض النظر عن أطوال الأضلاع أو زوايا المتوازي، وتسهم هذه الخاصية في تحديد الهندسة الداخلية لمتوازي الأضلاع وتساعد في تحديد الزوايا والأبعاد الأخرى للشكل.

المحيط والمساحة في متوازي الأضلاع

يُعد المحيط والمساحة من المفاهيم الأساسية في الهندسة ويستخدمان لحساب المقادير الهندسية المختلفة.

1. حساب محيط متوازي الأضلاع

المحيط هو طول الخط الذي يحيط بمتوازي الأضلاع. في حالة متوازي الأضلاع، يتكون المحيط من جمع أطوال الضلعين المتجاورين. لحساب المحيط، يمكن استخدام الصيغ التالية:

• محيط متوازي الأضلاع = طول الضلع الأول + طول الضلع الثاني + طول الضلع الأول + طول الضلع الثاني

• محيط متوازي الأضلاع = 2 × (طول الضلع الأول + طول الضلع الثاني)

2. حساب مساحة متوازي الأضلاع

المساحة هي المساحة الداخلية لمتوازي الأضلاع، وتُقاس بوحدة مربعة مثل المتر المربع أو السنتيمتر المربع. لحساب المساحة، يمكن استخدام الصيغة التالية:

"مساحة متوازي الأضلاع = طول القاعدة × الارتفاع" حيث يتم ضرب طول إحدى القواعد (القاعدة الصغرى أو القاعدة الكبرى) في الارتفاع المناظر لها.

على سبيل مثال، إذا كان لدينا متوازي الأضلاع طول قاعدته الصغرى 6 سم وارتفاعه 5 سم، يمكننا حساب مساحته عن طريق ضرب طول القاعدة في الارتفاع:

مساحة متوازي الأضلاع = 6 سم × 5 سم = 30 سم مربع.

ملحوظة: تأكد دائمًا من استخدام نفس وحدات القياس عند حساب المحيط والمساحة لضمان الدقة الصحيحة للإجابة.

شروط يجب توافرها في متوازي الأضلاع

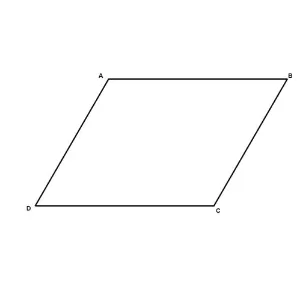
ليكون الشكل الهندسي متوازي الأضلاع، يجب توافر عدة شروط ومعايير، وهي كالتالي:

1. التطابق بين ضلعين متقابلين: يجب أن يكون لدينا ضلعان متقابلان في الشكل الهندسي يتطابقان في الطول والاتجاه، وهذا يعني أن الأضلاع المتقابلة يجب أن تكون لها نفس الطول وأن تكون متوازية لبعضها البعض.
2. التوازي بين الضلعين المجاورين: إضافةً إلى التطابق بين الضلعين المتقابلين، يجب أن يكون الضلعان المجاوران متوازيان لبعضهما البعض، وهذا يعني أن زوايا التقاء الضلعين المجاورين يجب أن تكون متساوية ومتوازية.
3. المجموعة الكاملة للزوايا: يجب أن يكون مجموع زوايا الشكل الهندسي الأربعة يساوي 360 درجة، وهذا يشير إلى أن الزوايا الأربعة في الشكل تكمل بعضها البعض لتكوين دورة كاملة.
4. الاستقامة: ينبغي أن تكون الأضلاع المتقابلة مستقيمة ومتوازية لبعضها البعض، ويعني ذلك أن خطوط الضلعين المتقابلين يجب أن تكون مستقيمة ومتوازية.