الزاوية المكملة لزاوية حادة تكون زاوية

تُعد الزوايا من أهم المفاهيم في علم الرياضيات والهندسة، إذ تُستخدم في وصف الأشكال وتحديد القياسات. ومن بين العلاقات المهمة بين الزوايا ما يُعرف بالزوايا المكملة، وهي زاويتان مجموع قياسهما يساوي 180. وتكمن أهمية هذه العلاقة في ربطها بين أنواع الزوايا المختلفة مثل الحادة والمنفرجة والقائمة. وفي هذا المقال في موقع مفاهيم نتعرف على إجابة سؤال الزاوية المكملة لزاوية حادة تكون زاوية هي؟

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• الزاوية المكملة لزاوية حادة تكون زاوية
• الزاوية المكملة لزاوية حادة تكون زاوية حادة منفرجة قائمة مستقيمة
• قياس الزاوية المكملة لزاوية 100 90 صح خطأ ؟
• تعريف الزاوية المكملة
• علاقة الزاوية المكملة بالأنواع الأخرى من الزوايا

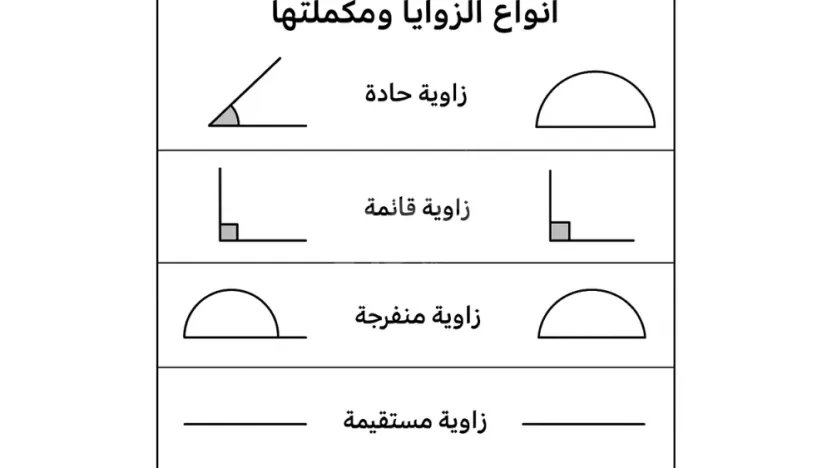
الزاوية المكملة لزاوية حادة تكون زاوية

الإجابة هي: حادة ✅.

• الزوايا المكملة: مجموعهما = 90
• إذا كانت لدينا زاوية حادة (أصغر من 90)، فمكملها سيكون: 90∘−(زاوية حادة)

وهذا الناتج يكون زاوية حادة أيضًا، لأن الفرق بين 90 وأي عدد أقل منه يظل أقل من 90.

مثال:

• زاوية = 30 (حادة).
• مكملها = 90−30=60 → حادة.

إذن: الإجابة الصحيحة: الزاوية المكملة لزاوية حادة تكون زاوية حادة.

الزاوية المكملة لزاوية حادة تكون زاوية حادة منفرجة قائمة مستقيمة

الإجابة هي: زاوية حادة

قياس الزاوية المكملة لزاوية 100 90 صح خطأ ؟

الإجابة هي: خطأ

• الزاويتان المكملتان: مجموعهما = 180.
• إذا كانت الزاوية = 100، فإن مكملها = 180−100=80
• إذن ليست 90، بل 80.
• لذلك: عبارة "قياس الزاوية المكملة لزاوية 100 يساوي 90" = خطأ.

تعريف الزاوية المكملة

• الزاويتان المكملتان هما زاويتان يكون مجموع قياسهما = 180.
• كل واحدة منهما تسمى مكملة للأخرى.

علاقة الزاوية المكملة بالأنواع الأخرى من الزوايا

مع الزاوية الحادة (< 90)

• إذا كانت الزاوية حادة (مثل 40)، فإن مكملها سيكون: 180−40=140
• وهو قياس زاوية منفرجة.
• إذن: مكملة الحادة → منفرجة.

مع الزاوية القائمة (= 90)

• إذا كانت الزاوية قائمة، فإن مكملها = 180−90=90
• أي زاوية قائمة أيضًا.
• إذن: مكملة القائمة → قائمة.

مع الزاوية المنفرجة (> 90 وأقل من 180)

• إذا كانت الزاوية منفرجة (مثل 120)، فإن مكملها = 180−120=60
• وهو قياس زاوية حادة.
• إذن: مكملة المنفرجة → حادة.

مع الزاوية المستقيمة (= 180)

• إذا كانت الزاوية مستقيمة، فإن مكملها = 180−180=0
• وهذه لا تعتبر زاوية هندسية بالمعنى المعتاد.
• إذن: مكملة المستقيمة = 0° → غير زاوية.