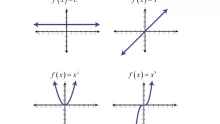
بحث عن العلاقات والدوال العكسية

تلعب العلاقات والدوال العكسية دورًا أساسيًا في علم الرياضيات، حيث تساعد في فهم كيفية ارتباط الكميات ببعضها البعض بشكل متبادل. تستخدم الدوال العكسية في مجالات متعددة مثل الفيزياء، والهندسة، وعلم الحاسوب، إذ تتيح لنا إيجاد القيم الأصلية بعد تطبيق عمليات معينة، وفي موقعكم مفاهيم نتعرف على بحث عن العلاقات والدوال العكسية وأهميتها.

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• بحث عن العلاقات والدوال العكسية
  • أولًا: مفهوم العلاقة والدالة
  • شروط وجود الدالة العكسية
  • خصائص الدوال العكسية
  • أمثلة على الدوال العكسية
  • كيف يمكن استخدام الدوال العكسية في الحياة الواقعية؟

بحث عن العلاقات والدوال العكسية

أولًا: مفهوم العلاقة والدالة

• العلاقة في الرياضيات هي مجموعة من الأزواج المرتبة التي تربط بين عناصر مجموعتين. يمكن تمثيل العلاقة كمجموعة من القيم المرتبطة ببعضها، مثل العلاقة بين درجات الحرارة والزمن أو بين الأعداد ومربعاتها.

ثانيًا: الدالة العكسية

• الدالة هي نوع خاص من العلاقات، حيث يرتبط كل عنصر في المجال بعنصر واحد فقط في المدى. بمعنى آخر، لكل قيمة إدخال (x) هناك قيمة إخراج واحدة فقط (y).

شروط وجود الدالة العكسية

لكي تمتلك الدالة f (x) دالة عكسية f−1 (x)، يجب أن تحقق الشرطين التاليين:

1.أن تكون الدالة متباينة (واحد لواحد - One-to-One):

• أي أنه لكل قيمتين مختلفتين x1 و x2 في المجال، فإن (f (x1) \= f (x2.
• بمعنى آخر، لا يمكن أن يكون لصورتين مختلفتين في المجال نفس القيمة في المدى.

2. أن تكون الدالة شاملة (Onto) على مدى معين:

• يجب أن تغطي جميع القيم الممكنة في المدى، أي أن لكل عنصر في المدى يوجد عنصر في المجال يحقق $f(x)$.

يمكن التحقق من أن الدالة متباينة باستخدام اختبار الخط الأفقي: إذا لم يقطع أي خط أفقي منحنى الدالة أكثر من مرة، فإن الدالة متباينة ويمكن أن يكون لها دالة عكسية.

خصائص الدوال العكسية

للدوال العكسية عدة خصائص مهمة تساعد في فهم سلوكها واستخدامها في مختلف التطبيقات، ومن أبرز هذه الخصائص:

• خاصية الانعكاس (التعويض): إذا كانت $f(x)$ دالة قابلة للعكس، فإن دالتها العكسية f−1(x) تحقق العلاقة: (f−1(x))=x، وهذه الخاصية تعني أن تطبيق الدالة ثم تطبيق دالتها العكسية يعيدنا إلى القيمة الأصلية.
• التناظر حول المستقيم $y=x:$بيانيًا، تكون الدالة العكسية انعكاسًا للدالة الأصلية حول المستقيم y=x ، أي أن كل نقطة (a,b) على منحنى $f(x)$ تصبح $(b,a)$ على منحنى f−1(x).
• وجود الدالة العكسية عند تحقق الشرط الواحد لواحد (One-to-One): لكي تمتلك دالة ما دالة عكسية، يجب أن تكون دالة متباينة (واحد لواحد)، أي أن كل قيمة في المجال تقابلها قيمة وحيدة في المدى. يمكن التحقق من ذلك باستخدام اختبار الخط الأفقي: إذا لم يقطع أي خط أفقي منحنى الدالة الأصلية أكثر من مرة، فهي تمتلك دالة عكسية.
• مجال الدالة الأصلية = مدى الدالة العكسية والعكس صحيح: إذا كانت الدالة الأصلية $f(x)$ تمتلك مجالاً D ومدى R، فإن الدالة العكسية f−1(x) يكون مجالها هو R ومدىها هو D.
• اشتقاق الدالة العكسية: إذا كانت $f(x)$ قابلة للاشتقاق ولها دالة عكسية f−1(x)، فإن مشتقة الدالة العكسية تُحسب كالتالي: f(f^-1(x))=f^-1(f(x))، وهذه الخاصية مهمة في حساب المشتقات في التفاضل والتكامل.
• استمرارية الدالة العكسية: إذا كانت الدالة الأصلية مستمرة ومتصلة، فإن دالتها العكسية تكون أيضًا مستمرة في مجالها.
• العمليات الجبرية على الدوال العكسية: أي أن الدالة العكسية لمركب دالتين هي مركب الدالتين العكسيين لكن بترتيب معاكس.

أمثلة على الدوال العكسية

من أهم الأمثلة على الدوال العكسية:

• إذا كانت الدالة الأصلية: f(x)=2x+3
• فإن الدالة العكسية تكون: f -1 (x) = (x - 3) / 2
• إذا كانت الدالة الأصلية: g(x)\=x3
• فإن الدالة العكسية تكون: √g−1(x) =3x​

الدوال العكسية لها تطبيقات واسعة في مختلف المجالات، حيث يتم استخدامها لاسترجاع القيم الأصلية أو عكس العمليات الرياضية، وإليك بعض الأمثلة على كيفية استخدامها في الحياة اليومية:

1. في الفيزياء والهندسة

• السرعة والزمن: إذا كانت العلاقة بين المسافة والزمن معطاة بدالة $s(t)=v\cdot t$ (حيث v السرعة)، فإن الدالة العكسية تساعد في إيجاد الزمن اللازم للوصول إلى مسافة معينة.
• درجة الحرارة: يتم تحويل درجات الحرارة بين وحدات مختلفة باستخدام دوال عكسية، مثل التحويل بين سلسيوس وفهرنهايت: F=C 5/9 +32 والدالة العكسية لها: C=5/9 ​(F−32)

2. في الاقتصاد والمالية

• حساب الفائدة المركبة: تستخدم الدوال العكسية لحساب معدل الفائدة أو الزمن اللازم لمضاعفة مبلغ معين في حساب مصرفي باستخدام معادلات مثل: A=P(1+r)t حيث $A$ هو المبلغ النهائي، $P$ المبلغ الأصلي، $r$ معدل الفائدة، و$t$ الزمن. بإيجاد الدالة العكسية، يمكن حساب الزمن اللازم لمضاعفة المبلغ.
• حساب الطلب والسعر: في علم الاقتصاد، يتم استخدام الدوال العكسية لحساب السعر بناءً على كمية الطلب، حيث يمكن أن تكون العلاقة بينهما معطاة بدالة مثل: $$P=f(Q)$$ حيث P هو السعر وQ هو الكمية المطلوبة.

3. في علم الحاسوب والبرمجة

• التشفير وفك التشفير: تستخدم الدوال العكسية في الخوارزميات المشفرة، مثل مفتاح التشفير وفك التشفير في تقنيات الأمان.
• مثال: تشفير البيانات باستخدام دالة $E(x)$ ثم استعادتها باستخدام دالتها العكسية E−1(x).
• الذكاء الاصطناعي والتعلم الآلي: في تحليل البيانات، تُستخدم الدوال العكسية لاسترجاع القيم الأصلية من البيانات المعالجة، مثل تحويل التنبؤات الاحتمالية إلى قيم فعلية.

4. في الطب والصيدلة

• حساب الجرعات الطبية: تستخدم الدوال العكسية لحساب الجرعة المطلوبة من الدواء بناءً على وزن المريض أو تركيز الدواء في الدم.
• مثال: إذا كانت الجرعة تحسب بدالة مثل $D=k\cdot W$ حيث $D$ هي الجرعة، و$W$ هو وزن المريض، فإن الدالة العكسية تُستخدم لحساب الوزن بناءً على الجرعة المعطاة
• أجهزة التصوير الطبي: في الأشعة والتصوير بالرنين المغناطيسي، تُستخدم الدوال العكسية لاستعادة الصور الأصلية من الإشارات المعالجة.

5. في علم الفلك والملاحة

• تحديد موقع الجسم السماوي: تُستخدم الدوال العكسية في حساب مواقع الكواكب والنجوم بناءً على بيانات الضوء والمسافة.
• نظام تحديد المواقع (GPS): تعتمد أنظمة GPS على الدوال العكسية لحساب الموقع الدقيق لمستخدم الهاتف بناءً على إشارات الأقمار الصناعية.