اكتشف كيفية حساب مساحة شبه المنحرف ومحيطه وارتفاعه بسهولة!
ما هو شبه المنحرف؟
شبه المنحرف (بالإنجليزية: Trapezoid) هو شكل هندسي ذو أربعة أضلاع، يتميز بوجود زوج من الأضلاع المتوازيتين. تعتبر هذه الأضلاع المتوازيتين من أهم خصائص شبه المنحرف. بالإضافة إلى ذلك، قد يكون لدى شبه المنحرف زوج من الزوايا المتقابلة المتساوية.
يمكن تصنيف شبه المنحرف بناءً على طول أضلاعه وزواياه.
- وفقًا للأطوال، قد يكون شبه المنحرف منتظمًا أو غير منتظم. في شبه المنحرف المنتظم، تكون جميع الأضلاع متساوية الطول، بينما في شبه المنحرف غير المنتظم، تكون الأضلاع غير متساوية الطول.
- بالنسبة للزوايا، فيكون الشبه المنحرف غير المنتظم زواياه غير متساوية، بينما في شبه المنحرف المنتظم، تكون جميع الزوايا متساوية.
ارتفاع شبه المنحرف
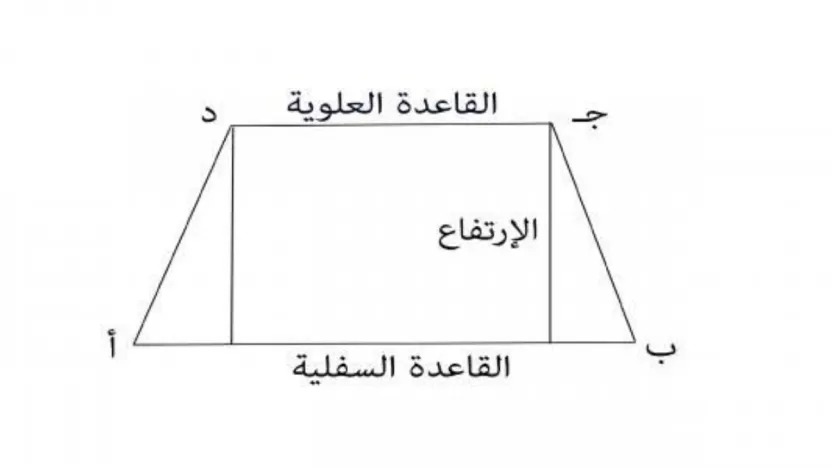
ارتفاع شبه المنحرف هو المسافة العمودية بين القاعدتين المتوازيتين (القاعدة الكبرى والقاعدة الصغرى)، ومن خصائص الارتفاع:
- هو أقصر مسافة تصل بين القاعدتين.
- يتم رسمه على شكل خط عمودي يبدأ من إحدى القاعدتين إلى الأخرى.
محيط شبه المنحرف
محيط شبه المنحرف هو مجموع أطوال جميع أضلاعه الأربعة.
قانون المحيط:
- المحيط=الضلع الأول+الضلع الثاني+الضلع الثالث+الضلع الرابع
الخطوات لحساب المحيط:
- قياس جميع أضلاع شبه المنحرف.
- جمع أطوال الأضلاع الأربعة.
مثال:
إذا كان لديك شبه منحرف أضلاعه كالتالي:
- القاعدة الكبرى = 12 سم،
- القاعدة الصغرى = 8 سم،
- الضلع الثالث = 5 سم،
- الضلع الرابع = 7 سم.
المحيط يحسب كالتالي:
المحيط=12+8+5+7=32 سم
أنواع شبه المنحرف وخصائصه
فيما يلي جدول يوضح أنواع شبه المنحرف:
| نوع شبه المنحرف | الخصائص |
|---|---|
| عام |
|
| مختلف الأضلاع |
|
| قائم الزاوية |
|
| متساوي الساقين |
|
حساب مساحة شبه المنحرف
يتم حساب مساحة شبه المنحرف بواسطة القانون التالي:
مساحة شبه المنحرف = [(طول القاعدة الأولى + طول القاعدة الثانية) / 2] × (الارتفاع)، حيث:
- طول القاعدة الأولى وطول القاعدة الثانية هما طول الضلعين المتوازيين في شبه المنحرف.
- الارتفاع هو المسافة العمودية بين القاعدتين المتوازيتين في شبه المنحرف.
لحساب مساحة شبه المنحرف، يتم جمع طول القاعدة الأولى وطول القاعدة الثانية وقسمتهما على 2، ثم يتم ضرب الناتج بالارتفاع. على سبيل المثال، إذا كان لدينا شبه منحرف بطول قاعدة أولى قيمتها 6 وطول قاعدة ثانية قيمتها 8 وارتفاع قيمته 5، يمكن حساب مساحته على النحو التالي:
مساحة شبه المنحرف = [(6 + 8) / 2] × 5 = (14 / 2) × 5 = 7 × 5 = 35 وحدة مربعة.
حساب ارتفاع شبه المنحرف متساوي الساقين
لحساب ارتفاع شبه المنحرف متساوي الساقين، يمكن استخدام الصيغة التالية:
ارتفاع شبه المنحرف = (2 × مساحة شبه المنحرف) ÷ (القاعدة الأولى + القاعدة الثانية)
في هذه الصيغة، يجب معرفة قيمة مساحة شبه المنحرف وقيم القاعدة الأولى والقاعدة الثانية للشبه المنحرف. مثلاً، إذا كان لدينا شبه منحرف متساوي الساقين بمساحة قيمتها 24 وطول قاعدته الأولى والثانية هو 6، يمكن حساب الارتفاع على النحو التالي:
ارتفاع شبه المنحرف = (2 × 24) ÷ (6 + 6) = 48 ÷ 12 = 4 وحدات.
قانون مساحة شبه المنحرف متساوي الساقين
يقول قانون مساحة شبه المنحرف متساوي الساقين إن مساحة هذا الشكل يساوي متوسط أطوال القاعدة والجزء العلوي (الجوانب المتوازية) مضروبًا في الارتفاع.
صيغة قانون مساحة شبه المنحرف متساوي الساقين هي كالتالي:
مساحة شبه المنحرف = (القاعدة الأولى + القاعدة الثانية) ÷ 2 × الارتفاع
هنا يتم حساب مساحة شبه المنحرف بجمع طول القاعدتين وقسمها على 2، ثم يتم ضرب الناتج في الارتفاع. على سبيل المثال، إذا كان لدينا شبه منحرف متساوي الساقين بطول قاعدة أولى وثانية قيمتهما 4 وارتفاع قيمته 6، يمكن حساب مساحته على النحو التالي:
مساحة شبه المنحرف = (4 + 4) ÷ 2 × 6 = 8 ÷ 2 × 6 = 4 × 6 = 24 وحدة مربعة.
محيط شبه المنحرف
يكون حساب محيط شبه المنحرف المتساوي الساقين باستخدام القانون التالي:
محيط شبه المنحرف = 2 × (طول الضلع الغير المتوازي) + (طول القاعدة الأولى + طول القاعدة الثانية)
في هذه الصيغة، يجب معرفة طول الضلع غير المتوازي وقيم القاعدة الأولى والقاعدة الثانية للشبه المنحرف. على سبيل المثال، إذا كان لدينا شبه منحرف متساوي الساقين بطول ضلع غير متوازي يساوي 5 وقاعدة أولى وثانية بطول 3، يمكن حساب المحيط على النحو التالي:
محيط شبه المنحرف = 2 × 5 + (3 + 3) = 10 + 6 = 16 وحدة.
مساحة شبه المنحرف غير المنتظم
لحساب مساحة شبه المنحرف غير المنتظم، نستخدم القاعدة العامة لمساحة شبه المنحرف:
- المساحة=1/2×(القاعدة الكبرى+القاعدة الصغرى)×الارتفاع
الخطوات:
- تحديد القاعدتين: القاعدة الكبرى والقاعدة الصغرى هما الضلعان المتوازيان في شبه المنحرف.
- تحديد الارتفاع: الارتفاع هو المسافة العمودية بين القاعدتين.
مثال عملي:
إذا كان لديك شبه منحرف غير منتظم بحيث:
- القاعدة الكبرى = 10 سم،
- القاعدة الصغرى = 6 سم،
- الارتفاع = 5 سم،
- المساحة=1/2×(10+6)×5= 1/2×16×5=40 سم2
إذا كان الشكل أكثر تعقيدًا ويتضمن أضلاعًا غير متوازية، يمكن تقسيمه إلى أشكال أصغر (مثل مثلثات ومستطيلات) وحساب مساحة كل جزء على حدة.
الأخطاء الشائعة في حساب مساحة شبه المنحرف وكيفية تجنبها
عند حساب مقدار مساحة شبه المنحرف، هناك بعض الأخطاء الشائعة التي قد تحدث، إليك بعض هذه الأخطاء وكيفية تجنبها:
- خطأ في استخدام الأبعاد: قد يحدث خطأ عند استخدام أبعاد غير صحيحة للقاعدة أو الارتفاع، لهذا تأكد من قياس الأبعاد بدقة واستخدام نفس وحدات القياس في الحسابات.
- عدم جمع القاعدتين بشكل صحيح: في بعض الأحيان، يتم جمع قيمة القاعدة الأولى والثانية بشكل غير صحيح أو تفويت إحدى القيمتين، فتأكد من إجراء العملية الحسابية بدقة والتأكد من جمع كلا القيمتين.
- استخدام القانون الخاطئ: يؤدي استخدام قانون خاطئ لحساب مساحة شبه المنحرف إلى إجابة غير صحيحة، فتأكد من استخدام القانون الصحيح المناسب لنوع الشبه المنحرف المطلوب حساب مساحته.
- عدم ترتيب الأبعاد بشكل صحيح: قد يحدث خطأ عند ترتيب الأبعاد في الصيغة الرياضية الصحيحة، لذلك تأكد من وضع الأبعاد في المكان الصحيح في الصيغة وترتيبها بالتسلسل الصحيح.
- عدم التحقق من الإجابة: بعد القيام بالحسابات، تأكد من مراجعة الإجابة والتحقق منها بشكل دقيق، فقد يكون هناك خطأ بسيط في الحسابات يؤثر على النتيجة النهائية.
للإستفادة من هذا المقال انسخ الرابط
https://mafahem.com/sl_20087