أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟

في عالم الهندسة الفراغية، تتنوع الأشكال ثلاثية الأبعاد التي ندرسها، مثل الأهرامات والمنشورات، ولكل منها خصائص فريدة تميّزها. من بين هذه الأشكال، يأتي الهرم الخماسي والمنشور الثلاثي كنموذجين مهمين يجمع بين خصائص مشتركة وفروقات بارزة. السؤال المطروح: أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟ يعد فهم هذه الصفات خطوة أساسية لتعميق المعرفة الهندسية وربط المفاهيم بشكل عملي، وهذا ما نتعرف عليه في هذا المقال في موقع مفاهيم.

للنشر

واتس اب شارك غرد شارك

جدول المحتويات

• أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟
• أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟ عدد القاعدات عدد الأحرف عدد الوجوه عدد الرؤوس؟
• الهرم الخماسي و المنشور الثلاثي
  • 1. الهرم الخماسي (Pentagonal Pyramid)
  • خصائص الهرم الخماسي (Pentagonal Pyramid):
  • حساب حجم الهرم الخماسي (Pentagonal Pyramid):
  • 2. المنشور الثلاثي (Triangular Prism)
  • خصائص المنشور الثلاثي (Triangular Prism)
  • حساب حجم المنشور الثلاثي (Triangular Prism)
• الصفات التي تجمع بين الهرم الخماسي والمنشور الثلاثي

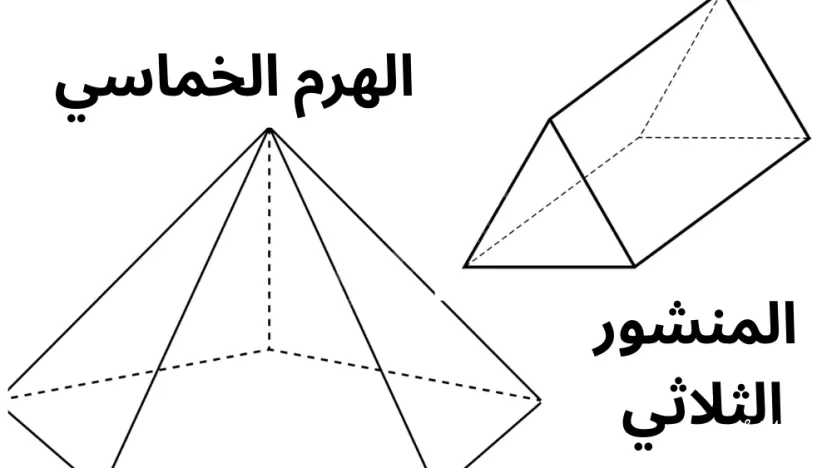
أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟

الإجابة هي: ✅ عدد الرؤوس.

• إذ أن الهرم الخماسي له قاعدة خماسية (5 أضلاع) وله 1 رأس علوي، مما يعطيه: عدد الرؤوس = 6 (5 رؤوس القاعدة + 1 رأس علوي)
• المنشور الثلاثي له قاعدتان مثلثيتان، وكل مثلث له 3 رؤوس: عدد الرؤوس = 6 (3 رؤوس القاعدة × 2)
• إذًا، كلاهما له 6 رؤوس.

أي الصفات الآتية تجمع بين الهرم الخماسي و المنشور الثلاثي؟ عدد القاعدات عدد الأحرف عدد الوجوه عدد الرؤوس؟

الإجابة الصحيحة: عدد الرؤوس.

• الهرم الخماسي يحتوي على 5 رؤوس في القاعدة بالإضافة إلى رأس واحد في الأعلى، فيكون المجموع 6 رؤوس.
• المنشور الثلاثي يحتوي على 3 رؤوس في كل قاعدة (قاعدتان مثلثيتان)، أي 3 + 3 = 6 رؤوس.
• إذن، الصفة المشتركة بينهما هي أن كل منهما يحتوي على 6 رؤوس، بينما يختلفان في عدد القاعدات والأحرف والوجوه.

الهرم الخماسي و المنشور الثلاثي

إليكم معلومات هامة عن الهرم الخماسي والمنشور الثلاثي وتشمل التعريف والخصائص و طريقة حسابهم والفرق بينهم:

1. الهرم الخماسي (Pentagonal Pyramid)

• هو شكل هندسي ثلاثي الأبعاد يتكوّن من قاعدة على شكل خماسي الأضلاع (أي له 5 أضلاع).
• له رأس واحد (قمة الهرم) يتصل بجميع رؤوس القاعدة.
• يتكوّن من: قاعدة خماسية - 5 أوجه مثلثة جانبية (كل وجه مثلثي يربط بين قمة الهرم وضلع من القاعدة).

خصائص الهرم الخماسي (Pentagonal Pyramid):

• القاعدة: خماسي الأضلاع (5 أضلاع).
• الرؤوس: 6 رؤوس (5 رؤوس القاعدة + رأس القمة).
• الأوجه: 6 أوجه (1 قاعدة خماسية + 5 أوجه مثلثة جانبية).
• الحواف: 10 حواف (5 في القاعدة + 5 من القاعدة إلى القمة).
• القمة: يوجد رأس واحد (قمة الهرم).
• الأوجه الجانبية: مثلثة الشكل، تلتقي في نقطة القمة.
• نوع الشكل: متعدد السطوح (Polyhedron).

حساب حجم الهرم الخماسي (Pentagonal Pyramid):

• الهرم حجمه = (1/3) × مساحة القاعدة × ارتفاع الهرم
• مساحة القاعدة الخماسية = (5 × جانب القاعدة × ارتفاع المثلث الناتج) ÷ 2،أو يمكن حسابها باستخدام صيغة مساحة المضلع المنتظم (إذا كانت القاعدة منتظمة).
• ارتفاع الهرم = المسافة العمودية من القمة إلى مستوى القاعدة.

2. المنشور الثلاثي (Triangular Prism)

• هو شكل هندسي ثلاثي الأبعاد يتكوّن من قاعدتين مثلثيتين متطابقتين وموضوعة بشكل موازٍ لبعضهما.
• يربط بين القاعدتين 3 أوجه مستطيلة (جانبية).
• يتكوّن من: قاعدتان مثلثيتان - 3 أوجه جانبية مستطيلة.

خصائص المنشور الثلاثي (Triangular Prism)

• القواعد: مثلثتان متطابقتان ومتوازيتان.
• الرؤوس: 6 رؤوس (3 رؤوس في كل قاعدة).
• الأوجه: 5 أوجه (2 قواعد مثلثية + 3 أوجه جانبية مستطيلة).
• الحواف: 9 حواف (3 في كل قاعدة + 3 حواف بين القاعدتين).
• القمة: لا يوجد رأس قمة.
• الأوجه الجانبية: مستطيلة الشكل ومتعامدة على القاعدتين.
• نوع الشكل: متعدد السطوح (Polyhedron).

حساب حجم المنشور الثلاثي (Triangular Prism)

• حجم المنشور = مساحة القاعدة × ارتفاع المنشور
• مساحة القاعدة المثلثية = (1/2) × قاعدة المثلث × ارتفاع المثلث
• ارتفاع المنشور = المسافة بين القاعدتين (طول المنشور).

الفرق الأساسي بين الهرم الخماسي والمنشور الثلاثي

• الهرم له قاعدة واحدة ورأس واحد.
• المنشور له قاعدتان متماثلتان ووجوه جانبية بينهما.

الصفات التي تجمع بين الهرم الخماسي والمنشور الثلاثي

التشابه والاختلاف بين الهرم الخماسي والمنشور الثلاثي:

• كلاهما أشكال منتظمة ثلاثية الأبعاد تتكوّن من مضلعات فقط، بدون جوانب أو زوايا مستديرة، مما يميزها عن الأشكال الكروية أو الأسطوانية.
• هما من متعددات السطوح بسبب وجود قواعد وجوانب مضلعة.
• يتلاقى جميع الوجوه الجانبية عند القاعدة أو القواعد.

الفرق الأساسي بين الهرم والمنشور: